
C2: The sequence should be easy to generate (for fast encryption). C1: The period should be very long (~ 10 50 at a minimum). The autocorrelation is out-of-phase if p does not divide k.įurthermore, to be of practical use for cryptologists we would require: G3: The out-of-phase autocorrelation AC(k) has the same value for all k.ĪC(k) = (Agreements - Disagreements)/p where we are comparing a sequence of period. Moreover, for any length, half the runs are blocks and the other half gaps. G2: Half the runs in a period have length 1, one-quarter have length 2. G1: The number of zeros and ones should be as equal as possible per period. What properties should a pseudo-random sequence have to make it look like a random Period sequences, called pseudo-random sequences. Since the finiteness forces the sequence to be periodic. However, no algorithm using a finite state machine can produce a truly random sequence, 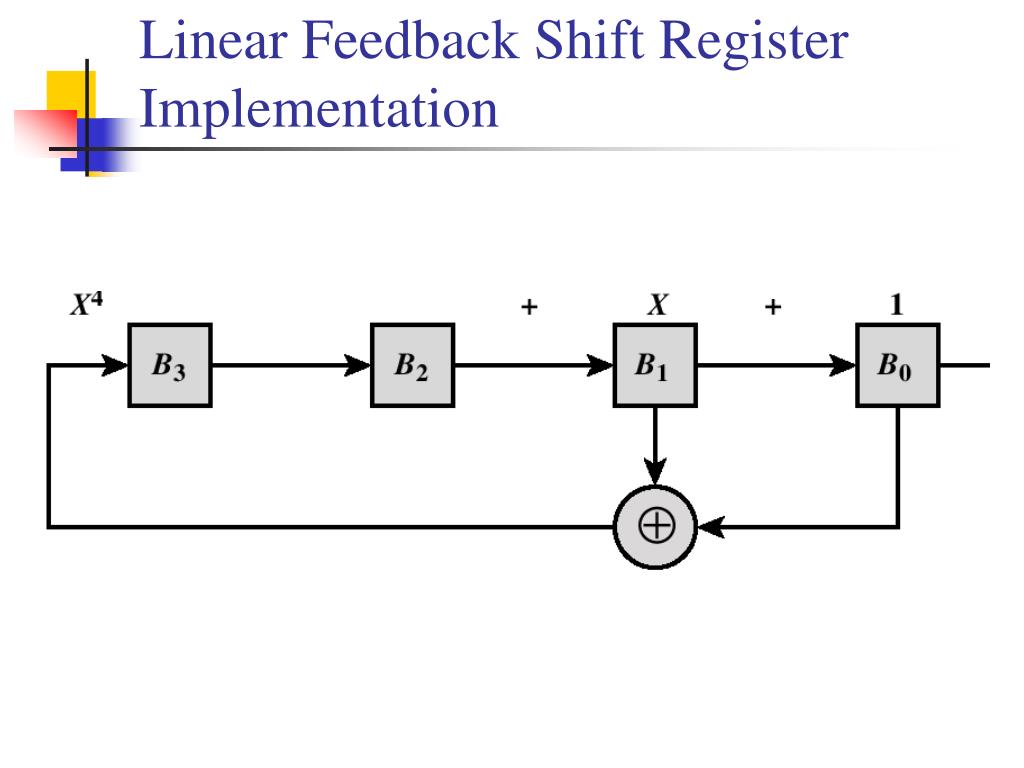
Generate the random sequence needed as the key (transfer of only a short seed would then be The key distribution problem for One-Time Pad suggests that one might use an algorithm to

Linear Feedback Shift Registers Linear Feedback Shift Registers








